오늘은 플라톤의 도형[Platonic Solids]이라 불리리는 ‘정다면체’라는 도형에 대해서 소개드리려고 합니다.
목차
1. 정다면체[Platonic Solids]란?
정다면체는 아래의 세 가지 조건을 모두 만족하는 입체도형입니다.
1) 모든 면이 똑같은 모양의 정다각형으로 이루어져 있습니다.
정다각형은 정삼각형, 정사각형, 정오각형처럼 변의 길이와 각의 크기가 모두 같은 도형을 말합니다. 정다면체는 모두 합동인 정다각형으로 만들어집니다.
2) 각 꼭짓점에 모이는 면의 개수가 같습니다.
어떤 꼭짓점에는 면이 3개가 모이고, 다른 꼭짓점에는 4개가 모이고… 이렇게 제멋대로 모이는 게 아니라, 모든 꼭짓점에 정확히 똑같은 수의 면이 모여 있어야 합니다.
3) 어디서 봐도 볼록한 모양입니다.
도형의 모든 부분이 바깥으로 볼록 튀어나와 있는 도형입니다.
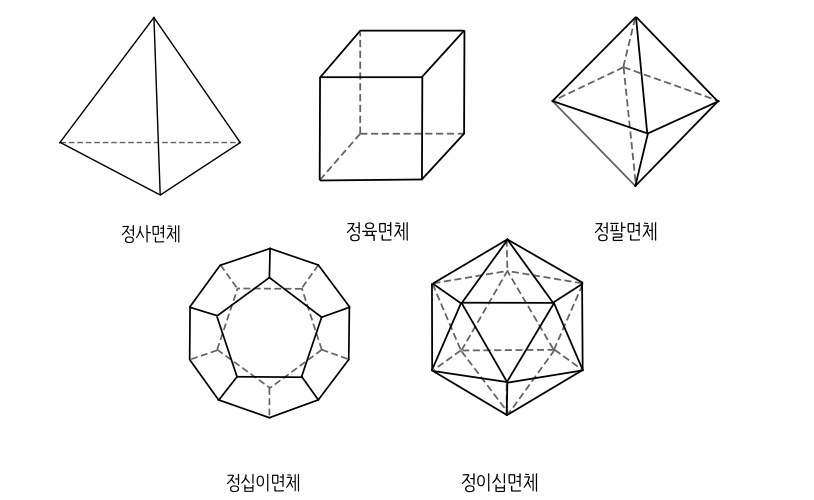
위의 까다로운 세가지 조건을 만족하는 정다면체는 정사면체, 정육면체, 정팔면체, 정십이면체, 정이십면체 이렇게 5개뿐입니다.
2. 플라톤과 정다면체
신비로운 5개의 정다면체는 아주 오래전 고대 그리스의 철학자 플라톤도 깊이 있게 연구를 했습니다. 그래서 정다면체를 플라톤의 입체(Platonic Solids)라고 합니다. 플라톤은 이 5가지 도형이 우주를 구성하는 기본적인 원소와도 관련이 있다고 생각했습니다.
- 정사면체: 불, 뜨거움, 예리함을 상징
- 정육면체: 흙, 안정성, 신뢰성을 상징
- 정팔면체: 공기, 경쾌함, 공중을 나는 능력
- 정이십면체: 물, 유동성, 불확정성을 상징
- 정십이면체: 우주 또는 천상, 우주의 완전성을 상징
과학이 지금처럼 발달하지 않은 고대의 철학적인 해석이지만, 고대의 사람들이 기하학적인 도형의 성질에 대해 깊이 생각했음을 엿볼 수 있습니다.
3. 정다면체가 다섯 종류만 존재하는 이유
왜 수많은 정다각형들이 있는데, 정다면체는 딱 5개밖에 없을까요?
입체 도형이 되기 위한 조건을 먼저 생각해보면 그 이유를 쉽게 짐작할 수 있습니다. 입체도형이 되기 위해서는 다음과 같은 조건을 만족시켜야 합니다.
조건 1_최소 3개의 면이 만나야만 하나의 꼭짓점이 만들어집니다.
조건 2_각 꼭짓점에 모인 면들의 각도의 합은 360도보다 작아야 합니다.
입체도형을 만들려면 평평하게 펴진 면을 이어붙여야 하는데 만약 한 꼭짓점에 모인 면들의 각도를 모두 더했는데 360도가 되어버리면 면이 평평하게 펼쳐져 버려서 입체도형을 만들 수 없습니다. 360도가 넘으면 오목한 부분이 생기거나 뾰족한 모양으로 변하게 되는등 모든 면이 볼록한 모양의 입체도형이 되지 않습니다.
정다각형의 한 내각의 크기를 생각해보면
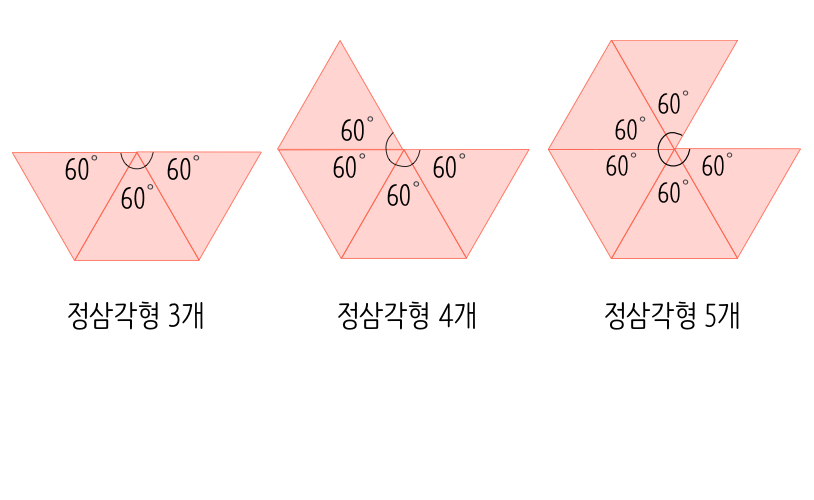
1) 정삼각형: 한 각이 60도
- 한 꼭짓점에 3개 모이면 60˚×3=180˚ (정사면체) – 입체 도형
- 한 꼭짓점에 4개 모이면 60˚×4=240˚ (정팔면체) – 입체 도형
- 한 꼭짓점에 5개 모이면 60˚×5=300˚ (정이십면체) – 입체 도형
- 한 꼭짓점에 5개 모이면 60˚×6=360˚ – 평면 (입체도형이 되지 않음)
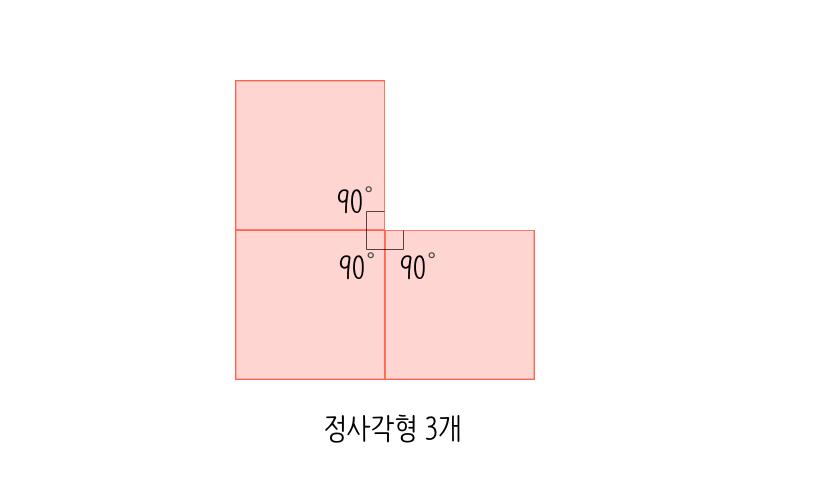
2) 정사각형: 한 각이 90도
- 한 꼭짓점에 3개 모이면 90˚×3=270˚ (정육면체) – 입체 도형
- 한 꼭짓점에 4개 모이면 90˚×4=360˚ – 평면 (입체도형이 되지 않음)
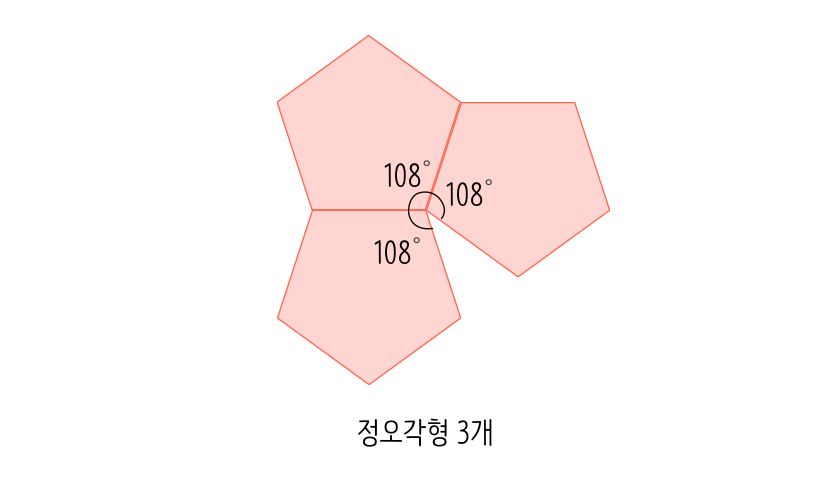
3) 정오각형: 한 각이 108도
- 한 꼭짓점에 3개 모이면 108˚×3=324˚ (정십이면체) – 입체 도형
- 한 꼭짓점에 4개 모이면 108˚×4=432˚ – 360도를 넘어버려서 볼록한 모양으로 만들 수 없음.
4) 정육각형 이상
정육각형은 한 각의 크기가 120도인데 3개만 모여도 360도가 되어버립니다. 적어도 3개는 한 점에서 모여야 입체도형이 되는데 3개만 모여도 평면이 되어버리니 정육각형보다 큰 정다각형은 정다면체의 면으로 만들 수 없습니다.
따라서 정오각형보다 각이 많은 다각형을 사용해서는 정다면체를 만들 수 없다고 할 수 있습니다.
따라서 정다면체의 면으로 가능한 정다각형은 정삼각형, 정사각형, 정오각형이며, 이를 통해 정다면체를 만들면 정사면체, 정육면체, 정팔면체, 정십이면체, 정이십면체를 만들 수 있습니다. 표로 정리하면 아래와 같습니다.
| 정다면체 | 면의 모양 | 한 꼭짓점에서 모이는 면의 수 | 면의 개수(Face) | 꼭짓점의 개수(Vertex) | 모서리의 개수(Edge) |
|---|---|---|---|---|---|
| 정사면체 | 정삼각형 | 3 | 4 | 4 | 6 |
| 정육면체 | 정사각형 | 3 | 6 | 8 | 12 |
| 정팔면체 | 정삼각형 | 4 | 8 | 6 | 12 |
| 정십이면체 | 정오각형 | 3 | 12 | 20 | 30 |
| 정이십면체 | 정삼각형 | 5 | 20 | 12 | 30 |
4. V – E + F = 2 [오일러 공식]
볼록한 입체 도형에서 어떤 도형이든 상관없이 성립하는 재미있는 규칙이 있습니다. 이 규칙을 발견한 수학자 ‘레온하르트 오일러’의 이름을 따서 오일러 공식이라고도 부릅니다.
공식은 간단합니다.
$$ V – E + F = 2 $$
V: 꼭짓점의 개수, E: 모서리의 개수, F: 면의 개수
이 오일러 공식을 정다면체에 적용해보겠습니다.
정사면체는 꼭짓점(V) 4개, 모서리(E) 6개, 면(F) 4개로 4-6+4=2가 성립합니다. 나머지도 살펴보면 모두 2가 나온다는 사실을 확인할 수 있습니다.
| 정다면체 | 꼭짓점의 개수(V) | 모서리의 개수(E) | 면의 개수(F) | V-E+F |
|---|---|---|---|---|
| 정사면체 | 4 | 6 | 4 | 2 |
| 정육면체 | 8 | 12 | 6 | 2 |
| 정팔면체 | 6 | 12 | 8 | 2 |
| 정십이면체 | 20 | 30 | 12 | 2 |
| 정이십면체 | 12 | 30 | 20 | 2 |
이 공식을 사용하면 정다면체 뿐만 아니라 우리가 주변에서 볼 수 있는 축구공이나 피라미드, 직육면체 등 구멍이 뚤려있지 않고 바깥으로 볼록한 모양의 입체도형이라면 모두 이 공식이 성립합니다.
오일러 공식은 도형의 모양이나 크기와 상관없이 그 도형이 가지고 있는 근본적인 구조를 알려주는 규칙입니다. 오일러 공식은 ‘위상수학’이라는 수학분야에서 아주 중요한 역할을 합니다.
5. 주변에서 볼 수 있는 정다면체
정다면체는 우리 주변에서도 심심치않게 찾을 수 있습니다. 주사위는 대표적인 정육면체 모양이고, 소금이나 보석광물의 결정은 정육면체나 정팔면체의 모양을 닮기도 합니다. 눈에 보이지는 않지만 많은 바이러스의 머리부분이 정이십면체의 구조를 갖고 있습니다.
보드게임에서도 정다면체 모양을 활용한 주사위가 많습니다. 정다면체는 모든 면이 나올 확률이 같습니다. 그래서 여러 면 주사위(D4, D6, D8, D10, D12, D20 등)는 정다면체의 이름을 딴 주사위들이 있습니다. D4는 정사면체, D6는 정육면체, D8은 정팔면체, D12는 정십이면체, D20은 정이십면체 주사위입니다.

마무리
다양한 모양의 다면체가 있지만 모든 면이 정다각형으로 만들어진 정다면체는 다섯 가지 밖에 존재하지 않습니다. 그 사실이 정다면체의 특별함을 느끼게 해주는듯합니다.
이 글로 인해 즐거운 시간이 되셨길 바래요. 감사합니다.

