Magic Square라고 불리는 마방진에 대해 들어보셨나요? 이 글에서는 마법의 사각형이라고도 불리는 마방진에 대해서 소개를 해드리려고 합니다.
목차
1. 마방진(Magic Square)의 기원
마방진에 대한 가장 오래된 기록은 중국에서 등장합니다. 낙서 마방진의 기원에 대해서는 여러 가지 설이 있지만 그 가운데 한가지를 소개해드립니다. 옛 중국 하나라의 우왕이 홍수를 막기 위해 낙수의 물을 퍼내는 과정에서 거북이를 발견했습니다. 그 거북이의 등에 이상한 무늬가 그려져 있어 이상한 무늬를 신기하게 본 우왕이 그림으로 옮겨 둔 것이 오늘까지 전해지는 ‘낙서(洛書)’라고 알려진 3×3 마방진입니다. 도교의 개념과도 연관이 된 마방진은 과거부터 신비를 상징하는 수의 패턴으로 여겨졌습니다. 조선시대 최석정이 쓴 <구수략(九數略)>에도 9차 마방진이 등장하며, 동양은 물론 서양까지 퍼져나가 수학의 발전에 많은 영향을 끼쳤다고 합니다.
마방진은 정사각형의 모양의 격자 안에 숫자를 채우는 퍼즐인데, 규칙은 간단합니다. 가로줄, 세로줄, 그리고 두개의 대각선의 합을 모두 같게 만들어주어야 합니다.
예를 들어 3×3 마방진에서는 1~9까지의 숫자를 한 번씩만 사용하여 가로, 세로, 대각선의 합을 모두 같게 만듭니다. 아래와 같은 마방진을 만들 수 있습니다.
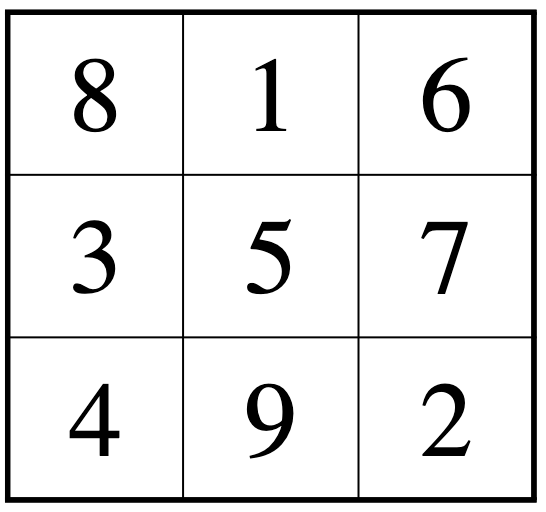
계산을 해보면 가로, 세로, 두 대각선의 숫자의 합이 15로 모두 같습니다.
$$ 가로: \; 8+1+6 = 15, \; 3+5+7=15, \; 4+9+2=15 $$
$$ 세로: \; 8+3+4=15, \; 1+5+9=15, \; 6+7+2=15 $$
$$ 두 대각선: \; 8+5+2=15, \; 6+5+4=15 $$
4×4 마방진은 1부터 16(4의 제곱), 5×5마방진은 1부터 25(5의 제곱)까지의 수를 채워 넣어 가로, 세로, 대각선의 합을 모두 같게 만든 것 입니다.
2. N차 마방진
이와 같은 방식으로 마방진은 무수히 만들 수 있는데 n차 마방진을 정의하면 아래와 같습니다.
$$ n차 \; 마방진이란? $$
$$ n \times n 정사각형 \; 안에 \; 1부터 \; n^2까지의 \; 숫자를 \; 배열하여 $$
$$ 가로, \; 세로, \; 대각선의 \; 합을 \; 같게\; 만든 \; 배열 $$
1) 1차 마방진
1차 마방진은 간단합니다. 1칸의 정사각형 안에 1만 써주면 되니까요. 단 1개만 존재합니다.

2) 2차 마방진
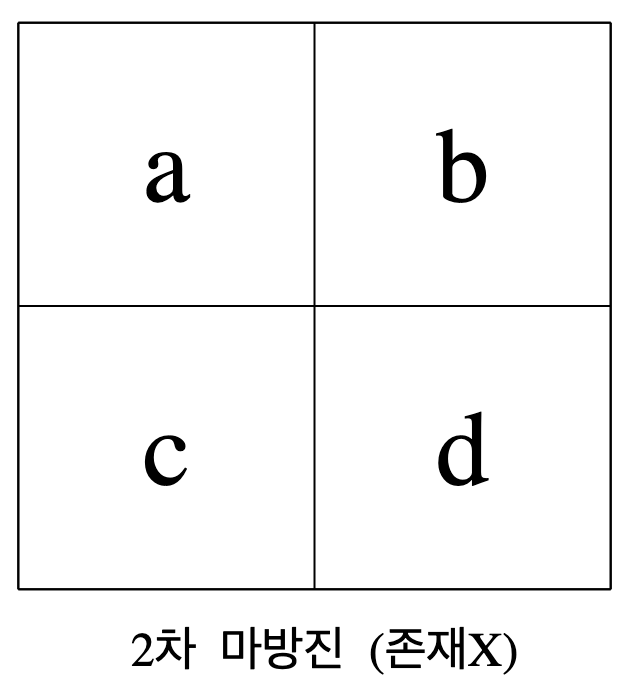
2차 마방진은 존재하지 않습니다. 아래 표를 보시면 간단하게 이해가 가능한데요.
마방진의 규칙에 따라 a + b = a + c가 되어야 하는데 그럼 b = c가 같다는 의미가 됩니다. a,b,c,d는 모두 다른 수여야 하는데 같아지기 때문에 존재할 수 없습니다.
3) 3차 마방진
회전하거나 대칭을 고려하면 3차 마방진은 한 가지가 존재합니다. 기본형을 회전하거나 대칭하여 3차 마방진을 만드실 수 있습니다. 3차 마방진의 경우 모든 행과 열, 대각선의 합은 15입니다.

4) 4차 마방진
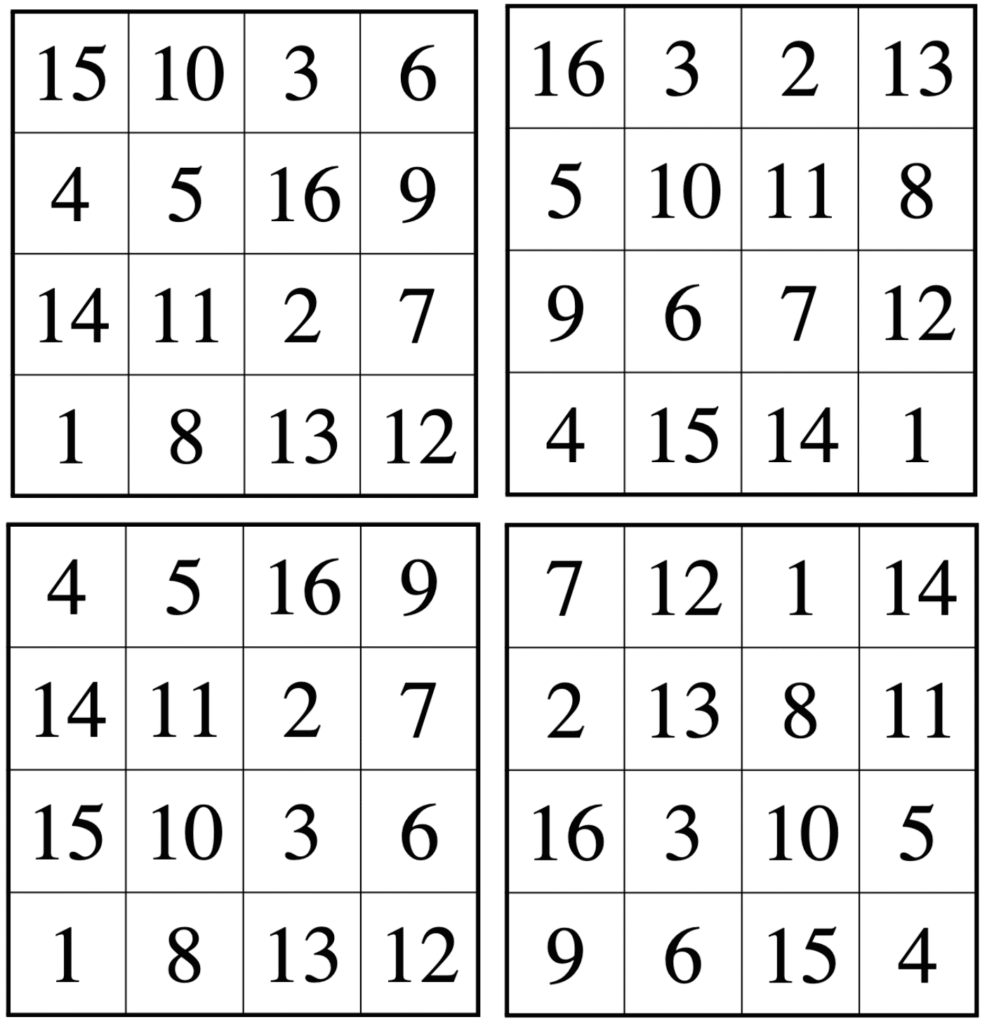
4차 마방진부터는 조금 복잡해집니다. 4차부터는 마방진의 개수가 증가하는데 4차 마방진은 880개가 존재를 한다고 합니다. 회전이나 대칭을 고려하면 기본적으로 다른 형태는 880개의 1/8인 110개 정도라고 해요. 4차 마방진의 모든 가로, 세로, 대각선의 합은 34입니다.
5) 5차 마방진
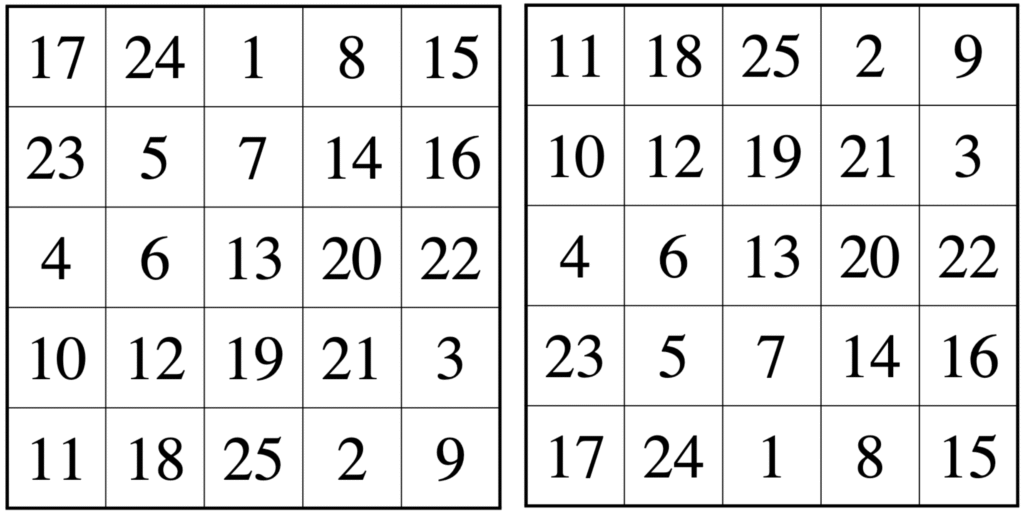
5차 마방진은 1~25까지의 수를 사용하여 가로, 세로, 대각선의 합을 모두 같게 만든 것입니다. 계산 결과에 따르면 275,305,224개(회전, 대칭 무시)가 존재한다고 해요.
6) 6차 마방진과 그 이후
6차 마방진은 이중 짝수 차수(4의 배수가 아닌 짝수 차수)에 해당하여 만드는 방법도 조금 더 복잡한 편입니다. (만드는 방법은 존재합니다.) 6차 마방진의 개수는 현재까지도 정확하게 계산이 되지 않았다고 해요. 4차 마방진에서 5차 마방진이 되었을 때 마방진의 개수가 기하급수적으로 늘어난 것처럼, 6차, 7차 마방진의 개수는 훨씬 더 커질 것으로 예상됩니다.
그 외에도 6차 마방진, 7차, 8차 마방진도 존재하며 마방진의 크기 제한이 없습니다. 2차 마방진만 존재하지 않을 뿐 더 큰 차수의 마방진은 무조건 존재한다고해요.
3. 마방진 상수(magic constant)
마방진에서 가로, 세로, 대각선의 합을 마방진 상수라고 부릅니다.
예를 들어 3차 마방진의 가로, 세로, 대각선의 합은 15이므로 15는 마방진 상수에 해당합니다. 4차 마방진 상수는 34, 5차 마방진 상수는 65입니다. 3차 마방진의 마방진 상수를 찾는 과정으로 마방진 상수를 구하는 방법을 알아보겠습니다.
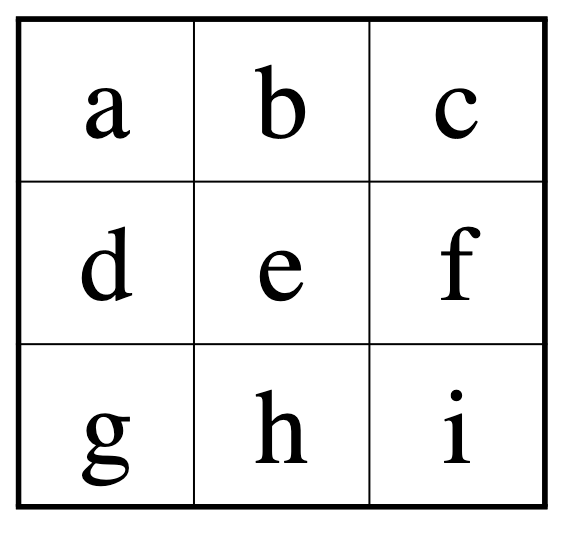
마방진 상수를 M이라고 하면 마방진의 규칙에 따라
$$ M = a+b+c=d+e+f=g+h+i $$
입니다.
마방진의 모든 수를 더하면 3M과 같습니다.
$$ 3M = a + b + c + d + e + f + g + h + i $$
3차 마방진에서 마방진 상수 M은 모든 수를 더한 값을 3으로 나눠준 것과 같습니다.
$$ M = \frac{a + b + c + d + e + f + g + h + i}{3} $$
1부터 9까지의 모든 수를 더하면 45가 되므로 45 나누기 3은 15라는 값을 구할 수 있습니다.
이를 일반화 하면 n차 마방진 상수는 다음과 같은 식으로 구할 수 있습니다.
$$ M(n) = \frac{1+2+3+4….+n^2}{n} $$
$$ 1부터 \; n^2까지 \;더한 \;값은 \;아래와;같습니다.$$
$$ 1 + 2 + 3 +…+n^2 = \frac{n^2 \times (n^2+1)}{2} $$
따라서
$$ M(n) = \frac{n^2 \times (n^2+1)}{2n} = \frac{n^3 + n}{2} $$
이 식에 맞춰 마방진 상수를 구해보면 다음과 같이 구할 수 있습니다. 2차 마방진이 존재하진 않지만 2차 마방진의 상수는 5라고 구할 수 있습니다. 2차 마방진이 존재하지 않기 때문에 5를 2차 마방진의 상수라고 부를 수는 없겠지만요.
$$ M(1) = 1 $$
$$ M(2) = 5 $$
$$ M(3) = 15 $$
$$ M(4) = 34 $$
$$ M(5) = 65 $$
$$ M(6) = 111 $$
마무리
소개드린 마방진 외에도 라틴방진이나 육각마방진 등 다양한 마방진이 있습니다. 마방진을 만드는 방법이나 다양한 신기한 성질을 가진 마방진도 존재합니다. 다음 기회에 소개를 해드릴게요!
감사합니다! : )

