목차
0! = 1 이라고?
수학을 공부하다 보면 직관적으로 말이 되지 않는 듯한 신기한 사실을 하나 알게 되었습니다. 바로 0! = 1이라는 사실입니다.
“아니, 0은 아무것도 없는데 어떻게 1이 될 수 있지?” 하고 의문을 가지고 그 이유들을 찾아보게 되었습니다.
이번 글에서는 팩토리얼(factorial)의 개념과 왜 0! = 1이 되는지에 대해 이야기해보려고 합니다. 다소 엄밀한 의미의 수학적 증명은 아닐 수 있지만 추론하는 과정을 유의깊게 살펴봐주시길 바랍니다.
먼저 팩토리얼이 낯설 수 있는 분들을 위해 팩토리얼의 개념부터 차근차근 알아보겠습니다.
팩토리얼이란?
팩토리얼은 어떤 수부터 1까지 차례대로 곱하는 것을 말합니다. 숫자 뒤에 !를 붙여서 표현합니다.
몇가지 예시를 살펴보겠습니다.
$$ 5! = 5 \times 4 \times 3 \times 2 \times 1 = 120 $$
$$ 3! = 3 \times 2 \times 1 = 6 $$
$$ 2! = 2 \times 1 $$
n!은 “n부터 1까지 모두 곱한 수” 입니다.
$$ n! = n \times (n-1) \times (n-2)….. \times 1 $$
팩토리얼은 주로 수학의 순열이나 조합등을 계산하거나 경우의 수를 계산할 때 많이 사용하는 수학기호입니다.
팩토리얼이 주로 사용되는 분야는 다음과 같습니다.
- 경우의 수 계산: 순서가 중요하거나 중요한 순서대로 배열하는 경우(순열)와 특정 순서 없이 뽑는 경우(조합) 등 다양한 경우의 수를 계산하는 데 사용
- 확률 계산: 경우의 수를 계산하여, 일이 일어날 확률을 계산할 때에도 팩토리얼이 활용
- 통계학: 통계학에서도 경우의 수와 관련된 계산을 위해 팩토리얼이 자주 사용
0!은 몇일까?
그렇다면 0!은 몇일까요? 직관적으로 생각해보면 0부터 0까지 곱해나가면 되니 0이라고 생각하실 수 있습니다.
하지만 0!의 값이 왜 1인지에 대해 몇 가지 방법으로 살펴보고자 합니다.
1) 곱하기를 이용한 방법
팩토리얼에는 다음과 같은 규칙이 있습니다.
$$ n!=n×(n−1)!$$
즉, 큰 수의 팩토리얼은 항상 작은 수의 팩토리얼을 포함하고 있습니다.
예를 들어,
$$ 10! = 10 × 9! $$
$$ 100! = 100 \times 99!$$
입니다.
다음과 같은 과정을 따라가면
$$ 4! = 4 \times 3! $$
$$ 3! = 3 \times 2! $$
$$ 2! = 2 \times 1! $$
$$ 1! = 1 \times 0! $$
1!은 분명히 1입니다. 그럼 1=1×0!의 식을 만족하기 위해서는 0! = 1이라는 결론이 나옵니다.
2) 나누기를 이용한 방법
다음은 나눗셈을 이용한 방법입니다.
2를 곱해주면 2배씩 커지면서 2의 지수는 하나씩 늘어납니다.
$$ 2^1 = 2 $$
$$ 2^2 = 4 $$
$$ 2^3 = 8 $$
$$ 2^4 = 16 $$
입니다. 반대로 2로 나누어주면 2의 지수는 하나씩 줄어들게 됩니다.
$$ 2^4 \div 2 = 2^3 $$
$$ 2^3 \div 2 = 2^2 $$
$$ 2^2 \div 2 = 2^1 $$
$$ 2^1 \div 2 = 2^0 = 1 $$
이 방법을 팩토리얼에 적용해보도록 하겠습니다.
$$ 4! \div 4 = 3! $$
$$ 3! \div 3 = 2! $$
$$ 2! \div 2 = 1! $$
$$ 1! \div 1 = 0! $$
1!은 1이므로 1 = 0!이 성립합니다.
3) 경우의 수로 생각해 보기
팩토리얼은 단순한 계산뿐 아니라 경우의 수를 세는 데 사용이 됩니다.
예를 들어, 3명의 아이들이 한 줄로 설 수 있는 방법의 가지 수는 3!=6가지입니다.
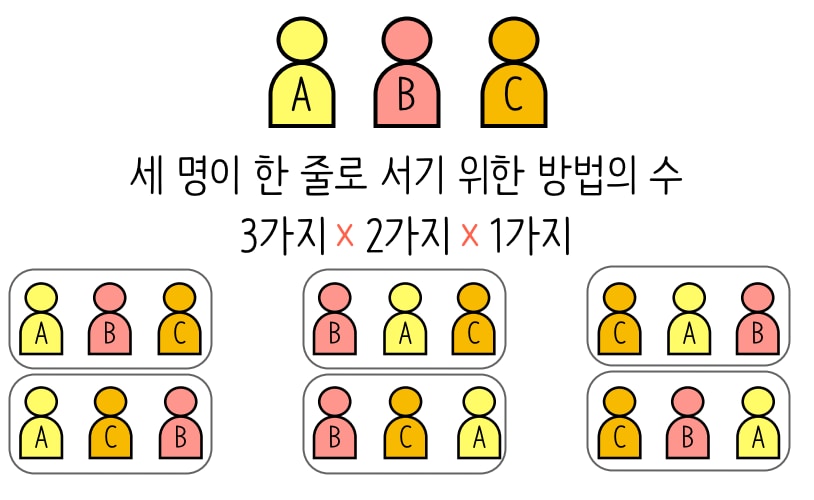
그렇다면 “아무도 줄을 서지 않는 경우”는 몇 가지 일까요?
아무도 줄을 서지 않는 방법은 아무도 서지 않는 것 오직 한 가지밖에 없습니다.
그래서 경우의 수의 관점에서 생각해보면 0! = 1이 됩니다.
빈 곱(empty product)의 원리
수학에서는 곱셈을 할 때, 곱할 것이 아무것도 없는 경우를 특별히 1로 정합니다. 이것을 “빈 곱(empty product)”이라고 불러요.
왜냐하면 곱셈에서 1은 곱하기의 기준이 되기 때문입니다. (예: a×1=a)
$$2^0 = 1 $$
2의 0제곱을 1이라고 정의하는 것도 비슷한 상황이라고 할 수 있습니다.
“0개의 수를 곱한다”라는 뜻인 0!은 1이 된다고 생각할 수 있습니다.
마무리
언뜻 보기에 0!은 0이라고 생각이 들 수 있습니다. 하지만 0!을 0이라고 정의해버리면 계산을 하는 과정에서 모순이 발생할 수 있습니다.
$$ 4! = 4 \times 3! $$
$$ 4! = 4 \times 3 \times 2! $$
$$ 4! = 4 \times 3 \times 2 \times 1! $$
$$ 4! = 4 \times 3 \times 2 \times 1 \times 0! $$
인데 이 때 0!이 1이 아니라면 계산 결과에 모순이 생기게 됩니다.
또 곱셈의 관점과 나눗셈의 관점, 경우의 수의 방식으로 논리를 따져보았을 때도 0! = 1로 정의하는 것이 자연스럽다는 것을 알 수 있습니다.
0! = 1은 억지로 정한 값이 아니라, 수학의 규칙과 생각들을 이어갈 때 꼭 필요한 자연스러운 정의라고 볼 수 있습니다.

