이번 글에서는 세 제곱수와 관련한 몇가지 사실들에 대해 탐구해보고자 합니다.
목차
세제곱수란?
세제곱수(Cube number)는 어떤 수를 세 번 곱한 수입니다.
Cube는 상자모양의 정육면체를 지칭하는 말입니다. 정육면체의 부피를 구할 때 세제곱수가 사용이 됩니다.
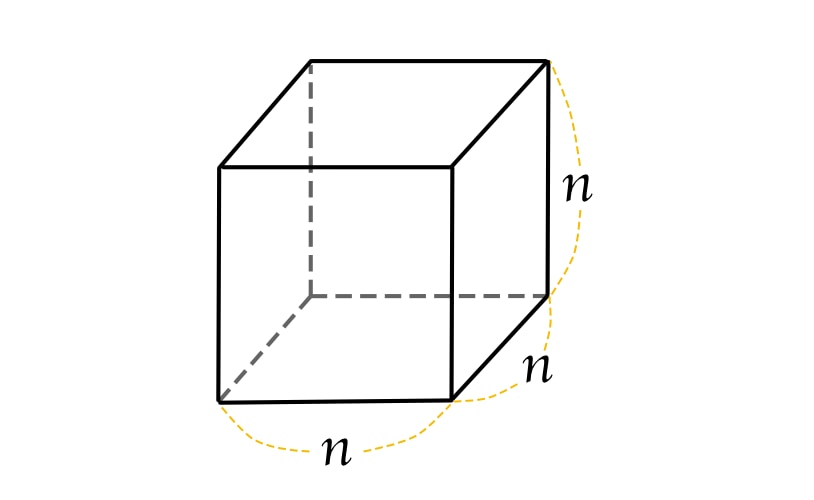
$$ n^3 = n \times n \times n $$
세제곱 수의 몇가지 예를 들어본다면 다음과 같은 수들이 있습니다.
$$ 2^3 = 8, \; 3^3=27,\; 4^3=64,\; 5^3=125 $$
세제곱수에 대한 몇가지 신기한 사실들
1. 모든 (454보다) 큰 수는 세제곱수의 합으로 만들 수 있다
놀랍게도, 454보다 큰 아주 큰 수들도 7개 이하의 세제곱수 합으로 표현할 수 있습니다.
몇 가지 예를 들어본다면 10000은
$$ 10000 = 21^3 + 9^3 + 2^3 + 1^3 + 1^3 $$
또는
$$ 10000 = 20^3 + 10^3 + 10^3 $$
의 5개 또는 3개의 세제곱수의 합으로 나타낼 수 있습니다.
1의 세제곱이 1이기 때문에 하나씩 더해나가면 어떤 수든지 만들어 낼 수 있겠지만 7개만으로 큰 수들을 모두 표현할 수 있다는게 신기합니다.
* 예외
단, 작은 수 중에는 몇 가지 예외가 있는데, 23과 239는 무려 9개의 세제곱수가 필요합니다.
$$ 23 = 2^3 + 2^3 + 1^3 + 1^3 + 1^3 + 1^3 + 1^3 + 1^3 + 1^3 $$
3의 세제곱은 27이라 2의 세제곱인 8을 두개 더할 수 밖에 없습니다.
24라면 2의 3제곱 3개로 간단히 나타낼 수 있겠지만 23은 그럴 수 없기 때문에 1을 부족한 부분만큼 채워주어야 합니다. 그래서 9개의 세제곱 수가 필요합니다.
239도 세제곱 수도 최소 9개의 합으로 나타낼 수 있는 수입니다.
6의 세제곱(216) 더하기 2의 세제곱(8)을 세번 하면 240이 됩니다.
$$ 6^3+2^3+2^3+2^3=240 $$
하나를 줄여야 하기 때문에 2의 세제곱 하나를 1의 세제곱 7개로 바꾸어야 합니다.
$$ 6^3+2^3+2^3+1^3+1^3+1^3+1^3+1^3+1^3+1^3=240 $$
최소 9개의 세제곱 수를 사용한다면 다음과 같이 나타낼 수 있습니다.
$$ 239 = 5^3 + 3^3 + 3^3 + 3^3 + 2^3 + 2^3 + 2^3 + 2^3 + 1^3 $$
예외를 정리하면 다음과 같습니다.
- 9개가 필요한 수(딱 2개): 23, 239
- 8개가 필요한 수(15개): 15, 22, 50, 114, 167, 175, 186, 212, 231, 238, 303, 364, 420, 428, 454
위의 17개를 제외한 모든 수는 7개 이하로 표현이 된다고해요.
이후 Siksek(2015/2016)이 이를 완전히 구체화하여 “454보다 큰 모든 정수는 7개 이하의 양의 세제곱수 합”임을 증명했다고 합니다.
2. 6의 배수와 세제곱수
모든 6의 배수는 단 4개의 세제곱수(부호를 허용할 경우)로 표현할 수 있습니다.
식은 이렇게 생겼어요.
$$ 6n = (n+1)^3 + (n-1)^3 – n^3 – n^3 $$
예를 들어 n이 1이라면
$$ 6 = 2^3 + 0^3 – 1^3 -1^3 $$
n이 100이라면
$$ 600 = 101^3 + 99^3 – 100^3 – 100^3 $$
으로 나타낼 수 있습니다. 이유는 간단합니다.
$$ (n+1)^3 = n^3 +3n^2 + 3n +1 이고$$
$$ (n-1)^3 = n^3 -3n^2 +3n -1 입니다. $$
$$ (n+1)^3 + (n-1)^3 = 2n^2 + 6n 입니다. $$
6n은 6의 배수이므로 아래와 같은 식으로 나타낼 수 있습니다.
$$ 6n = (n+1)^3 + (n-1)^3 – n^3 – n^3 $$
3. 세제곱수와 삼각수의 관계
삼각수(三角數, Triangular number)는 점을 삼각형 모양으로 배열했을 때 꼭 맞게 떨어지는 수를 말합니다.
아래처럼 점을 찍었을 때
•
• •
• • •
• • • •
• • • • •
1줄 일때는 점이 1개, 2줄일 때는 1+2 = 3개, 3줄일 때는 1+2+3=6개 이런 식으로 나타낼 수 있습니다.
n번째 삼각수는
$$ T_n = 1+2+3+4…..+(n-1)+n= \frac{n\times(n+1)}{2} $$
라고 할 수 있습니다.
세제곱 수는 이 삼각수와도 연관이 있습니다.
$$ n^3 = {T_n}^2 – {T_{n-1}}^2 $$
이란 식이 성립합니다. 말로 풀어 설명하면 n의 세 제곱수는 n번째 삼각수와 (n-1)번째 삼각수를 각각 제곱했을 때 큰 수와 작은 수의 차이라고 할 수 있습니다.
예를 들어 보면 4의 3승은 네번째 삼각수를 제곱한 수에서 세번째 삼각수를 제곱한 수를 빼준 값과 같다고 할 수 있습니다.
계산을 해보면
$$ 4^3 = {T_4}^2 – {T_3}^2$$
$$T_4 = 10, T_3 = 6 이므로, $$
$$ {T_4}^2=100, {T_3}^2=36 입니다. $$
$$ 4^3 = {T_4}^2 – {T_3}^2 = 100-36 = 64 $$
가 성립함을 알 수 있습니다.
이 방법을 일반화하여 연속된 삼각수를 각각 제곱하여 차이를 구하면 그 수는 세제곱 수라고 할 수 있습니다.
4. 특별한 회문(대칭) 세제곱수
세제곱수 중에는 회문수(palindrome, 거꾸로 읽어도 같은 수)도 있습니다.
예를 들면 11, 121, 1221과 같은 수들이 있어요.
11의 경우에는 제곱을 하거나 세제곱을 해도 회문수가 됩니다.
$$ 11^2 = 121, \; 11^3=1331, \; 11^4= 14641 … $$
모든 회문수를 제곱한다고 회문수가 되는건 아니지만 회문이 아닌 수를 세제곱해서 회문이 되는 수가 딱 하나 알려져 있습니다.
2201을 세제곱하면 다음과 같습니다.
$$ 2201^3=10662526601 $$
앞에서 읽어도 뒤에서 읽어도 10662526601인 회문수 입니다.
정리
이번 글을 정리를 해보면 다음과 같습니다.
1) 7개 이하의 세제곱수로 454보다 큰 수를 만들 수 있습니다.
2) 모든 6의 배수는 네 개의 세제곱수만을 이용해서 나타낼 수 있습니다.
3) 연속된 두 삼각수의 제곱의 차이는 세제곱 수 입니다.
4) 2201은 회문수가 아님에도 불구하고 세제곱을 해서 회문(대칭)이 되는 수가 있다.
세제곱이라고 하면 단순히 숫자를 세 번 곱한 수라고 생각할 수도 있지만 세제곱 안에는 재미있는 비밀들이 많이 숨어있습니다.

