도형의 합동과 성질 [5학년 2학기_3.합동과 대칭]

합동이란?

같은 모양의 비행기 비행모습 — 같은 모양의 비행기들이 편대비행을 하는 모습(출처:pexels.com)

일상에서 같은 모양의 물건이나 생김새를 보면 ‘똑같다’, ‘같은 모양이다.’ 라고 이야기를 합니다.

수학에서는 이런 관계를 ‘합동’(合同)’이라고 부릅니다. ‘합동’이라는 말은 한자로 합할 합(合), 같을 동(同) 자를 사용합니다. 즉, ‘서로 합쳐도(겹치면) 같은 모양이 된다’는 뜻입니다. 영어로는 합동을 ‘congruence’ 또는 ‘congruent’ 라고 합니다. “congruent figures”라고 하면 “합동 관계의 도형”이라는 뜻입니다.

그럼 도형이 합동이라는 건 구체적으로 어떤 의미일까요?

두 도형이 모양도 같고 크기도 같을 때, 그 둘을 합동한 도형이라고 합니다. 쉽게 말해, 하나의 도형을 들어서 돌리거나 뒤집거나 옮겼을 때 다른 도형 위에 정확히 겹쳐질 수 있다면 그것이 바로 합동이라고 합니다.

합동한 도형의 성질

합동한 도형은 다음과 같은 성질이 있습니다.

모양이 같다
크기가 같다.
겹쳤을 때 완전히 일치한다.

대응점, 대응변, 대응각

합동인 도형끼리는 각 점, 각 변, 각이 서로 짝을 이룬다는 특징이 있습니다. 이런 짝을 이루는 부분을 대응점, 대응변, 대응각이라고 합니다.

합동인 삼각형을 예로 들어보겠습니다.

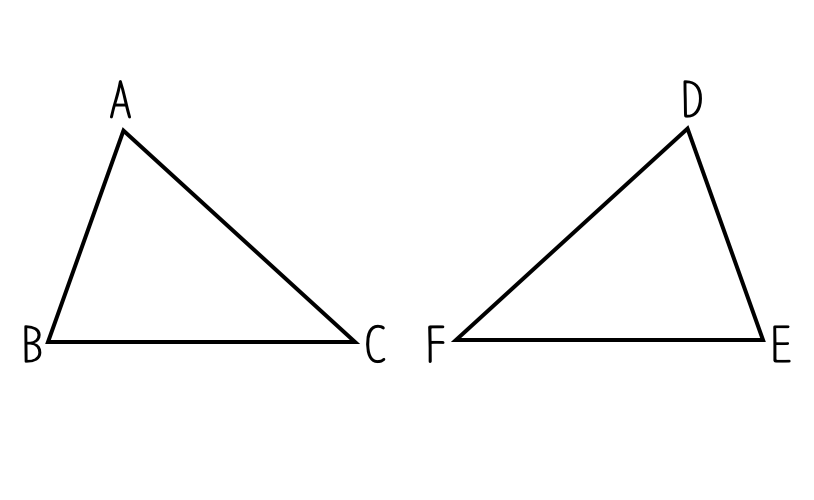
이때

A와 D, B와 E, C와 F는 서로 대응점(corresponding points)입니다.
AB와 DE, BC와 EF, CA와 FD는 대응변(corresponding sides)입니다.
∠A와 ∠D, ∠B와 ∠E, ∠C와 ∠F는 대응각(corresponding angles)입니다.

즉, 한 도형의 각 부분에 꼭 맞는 위치에 다른 도형의 부분이 대응하는 것입니다. 이 대응 관계를 바르게 짝지어야 두 도형이 정말로 합동인지 알 수 있습니다.

삼각형이 합동이 되는 조건

모든 도형 중에서 삼각형의 합동은 가장 기본적입니다. △ABC와 △DEF가 합동이라면 이렇게 표현합니다:

△ABC ≡ △DEF

삼각형은 세 변과 세 각으로 이루어져 있어서, 일부 정보만 같아도 두 삼각형이 완전히 같은 모양인지 알 수 있습니다.

삼각형이 합동이 되는 대표적인 조건은 다음과 같습니다.

세 변이 각각 같을 때 (SSS) → 세 변의 길이가 모두 같다면 두 삼각형은 합동입니다.
두 변과 그 사이의 각이 같을 때 (SAS) → 두 변의 길이가 같고 그 사이에 끼인 각이 같다면, 그 삼각형은 합동입니다.
두 각과 그 사이의 변이 같을 때 (ASA) → 한변의 길이가 같고 그 변의 양 끝각의 크기가 같으면 삼각형의 모양이 같아집니다.

이 조건들을 영어 약자로 기억하면 쉽습니다. S는 side(변), A는 angle(각)입니다.

예를 들어, 두 삼각형의 두 변의 길이와 그 사이의 각의 크기가 같다면(SAS), 그 두 삼각형은 합동입니다.

실생활 속의 합동

합동의 개념은 교과서 속에만 있는 것이 아니라 실생활에서 많이 접할 수 있습니다.

1. 거울 속의 모습

합동예시_거울에 비친 모습 — 거울에 비친 모습을 바라보는 원숭이 (출처:pexels.com)

거울에 비친 내 모습은 방향이 반대로 바뀐 합동이에요. 모양과 크기는 같지만 좌우가 뒤집혀 있습니다. 그래서 ‘대칭 합동’의 한 예라고 할 수 있어요.

2. 창문 유리나 타일

집이나 건물 벽에 있는 타일, 창문, 벽돌들은 대부분 같은 크기와 모양으로 만들어져 있습니다. 서로 포개면 딱 맞기 때문에 서로 합동인 도형들입니다.

3. 한 쌍의 양말 또는 신발

왼발, 오른발 신발은 방향은 다르지만, 서로 같은 모양과 크기로 만들어져 있습니다. 그래서 양말 한 쌍도, 신발 한 쌍도 합동 도형으로 볼 수 있습니다. 그 외에도 자동차 바퀴, 톱니바퀴, 종이를 반으로 접고 잘랐을 때 나오는 조각 등 다양한 합동인 도형을 찾아볼 수 있습니다.

마무리

‘합동’은 단순히 수학 속 용어가 아니라, 세상을 보는 또 하나의 눈이라고 볼 수 있습니다.

두 도형이 크기와 모양이 같을 때 우리는 그것을 ‘합동’이라고 부릅니다. 비행기가 하늘에서 같은 모양으로 줄지어 날아가는 모습, 거울 속의 내 얼굴, 벽에 가지런히 붙은 타일 하나하나 속에서도 합동의 원리를 찾아볼 수 있죠. 이처럼 합동은 규칙, 질서, 균형이 담긴 개념입니다. 우리 주변의 사물과 자연 속에서도 합동의 아름다움을 발견해보세요. 수학은 이렇게, 우리가 사는 세상 속에 언제나 숨어 있습니다.